Symmetries

Particle physicists are obsessed with symmetry in nature – but what they mean by that may be slightly different than what you imagine.

Let’s start by talking about symmetries we know about already, taking my face as an example. This is me:

• 

• 

• 

In the left photo, my face; in the middle photo, my face, mirrored from left to right, and on the right, mirrored from top to bottom. As you can see, my face is approximately left-right symmetric (let’s do me a favour for the moment!), and not at all top-bottom symmetric (thank goodness, how would I eat?).

Why is this insight useful? Well, even if I had never seen my face, knowing that it has (approximate) left-right symmetry but no top-bottom symmetry would tell me some things about it. For example:

• If I have a left eye, I must also have a right eye;
• I do not have an extra nose on my right cheek, unless I also have one on my left;
• I may have an extra eye on my forehead, but only if it is in the middle.

Mathematical mirrors

That’s a little silly of course, but bear with me. Now we have to take a mental leap, and that leap is generalizing what we mean by a mirror. Until now, I could have literally put a mirror to my face – now I’m going to use an internal, mathematical mirror.

Let’s take for example my comfort, as a function of temperature:

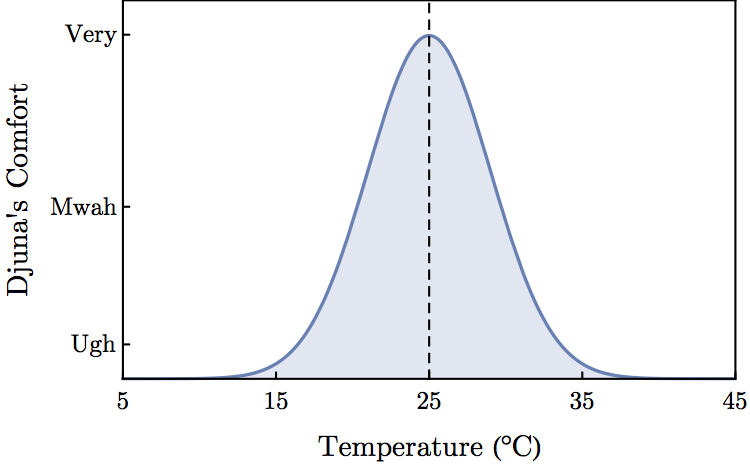
You can see that I am most comfortable at 25°C, and less comfortable at any other temperature. Quite the goldilocks, I know!

You can also see that if I place my mirror at 25°C, the graph looks the same. That is, my comfort is symmetric in a temperature-mirror, placed at 25°C. So: if I know how comfortable I am at 30°C, I also know how comfortable I am at 20°C.

The Standard Model

In much the same way, the group of currently known fundamental particles has a symmetry, only with a more complicated mirror: we call it SU(3)xSU(2)xU(1) or the Standard Model Group. That is, the laws of particle physics are symmetric with respect to reflections in the Standard Model Group. We have been developing this insight since the 1930s.

The symmetries of the Standard Model have been really useful, as they helped predict particles (for example, the top quark), in the same way that I could predict that I have a right eye because I also have a left eye. They also tell us which particles interact with each other, and which do not.

Given these successes of our Standard Model mirror, it may not be surprising that a popular way to look for new physics (for example, dark matter) consists of looking into new mirrors!

Featured image: work by the artist Teo Monsalve inspired by our interactions