Extra dimensions are pretty popular attributes of theories in particle physics (in fact, yours truly is currently working on such a theory!). But long before they became fashionable in physics, there are records of creative entrepreneurs and imaginative individuals captivated by the idea of a hidden world in another dimension. Some writers and visual artists developed our ideas in ways that were not only fascinating from an artistic perspective, but also very useful for visualisations of modern physics.

 

Most notable is Edwin Abbott Abbott, whose ideas preceded his contemporaries across fields by far. Edwin had (besides very funny parents that gave him his peculiar double name) a job as an English teacher and a mind for geometric exploration. In his 1884 novella Flatland the character Square lives in a 2D world (yes, “Flatland”) along with the other flat figures (triangles, and circles for instance). The inhabitants of Flatland also experience a 1D world (“Lineland”), whose occupants are points.

 

Like all flat figures, Square is amazed that the points are confined to thinking in their 1D lines, and that they cannot envisage the second dimension, which is so real to him. But that changes when he gets a visit from Sphere, who shows him a whole new world: 3D (“Spaceland”). Sadly, as Square comes back to his Flatland, no one believes him that Spaceland exists.[1]

 

It is not that the Flatlanders do not experience the 3D figures such as Sphere and his friends. But they do so in 2D, that is, through a cross section, when they float through Flatland, for example (I hope you are impressed by my paint skills):

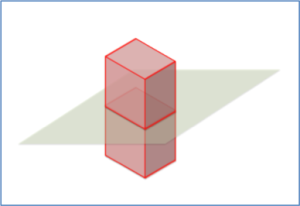
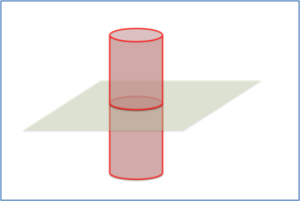
Now what is interesting about this is that we may experience extra dimensions in the same way. I know it’s hard to visualise,[2] but maybe you agree analogously that the (3+1) dimensional objects we perceive could theoretically be cross-sections of (3+…+1) dimensional objects. This is conceptually similar to how I use extra dimensions in my work.[3]

 

Abbot was far ahead of his time, and inspired many scientists and artists. And he still does: in my first year at university, my lecturer organised a special screening of Flatland, and I found it both explanatory and inspirational. To me, what Abbot managed to capture is that it is hard to tell what is limited: the number of dimensions, or our imagination. In the latter case, opening up a dialogue between contemporary physicists and creative individuals may not be such a bad idea.

 

In an upcoming post I will explore the topic of Extra dimensions through the eyes of visual artists. I am also working on an article for the Conversation about techniques for visualising 5D!

 

[1] Check out Flatland, the movie

[2] See this xkcd comic

[3] Similar, but not quite, I have to admit. In reality we integrate over the extra dimension, but I’ll spare you the details of that.